Работа с интерактивной лекцией
Прочитайте теоретический материал, во время чтения составьте тезисный конспект, выполните задания с открытым ответом (проверяются преподавателем).
Изучаем
В курсе Информатики и ИКТ рассматривается такая тема как «Поиск информации в Интернет». При решении определенного типа задач на эту тему удобно использовать круги Эйлера (диаграммы Эйлера — Венна).
Из курса математики нам известно, что рисунки в виде кругов, изображающих множества, используются очень давно. Одним из первых, кто пользовался этим методом, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц. В его черновых набросках были обнаружены рисунки с такими кругами. Лейбниц использовал их для геометрического объяснения логических связей между понятиями. Затем этот метод развил Леонард Эйлер.
Диаграммы Эйлера — Венна используются, прежде всего, в теории множеств как схематичное изображение всех возможных пересечений нескольких множеств.
Давайте проведём аналогию между хорошо нам известной из математики теорией множеств и логическими операциями, т. е. к логике высказываний применим математический аппарат.
Конъюнкция
Пересечением двух множеств и называется множество их общих элементов.
Пусть множество состоят из букв:
Пусть множество состоят из букв:
Эти множества имеют общий элемент: о.
С помощью диаграммы Эйлера — Венна можно графически изобразить множество
На диаграмме закрасим только ту область, которая соответствует логической единице (истине) в выходном столбце таблицы истинности. Дизъюнкция Объединением двух множеств Пусть множество С помощью диаграммы Эйлера — Венна можно графически изобразить множество
Результатом конъюнкции
Аналогичные рассуждения применим к следующей операции над множествами.
Пусть множество 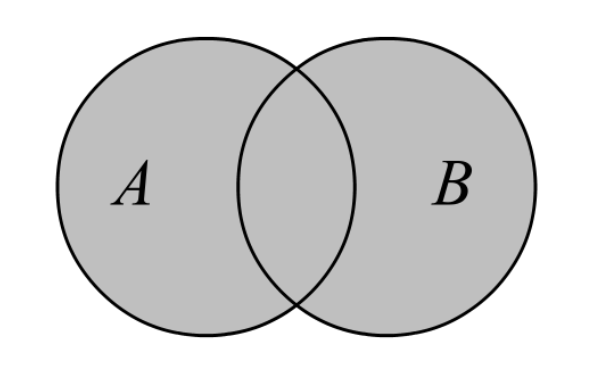
Дизъюнкция (логическое сложение):
Рассмотрим таблицу истинности:
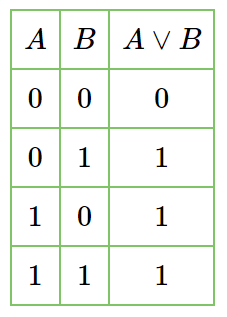
Действительно, закрашенными получаются все три области на диаграмме, которые соответствует логической единице (истине) в выходном столбце таблицы истинности.
Инверсия
В теории множеств логическому отрицанию (инверсии) соответствует операция дополнения к множеству.
Дополнение имеет смысл не для всех множеств, а только тогда, когда второе множество является подмножеством первого.
Рассмотрим частный случай. Пусть множество
Пусть множество
Пусть множество
Дополнение
Рассмотрим общий случай: дополнение некоторого множества
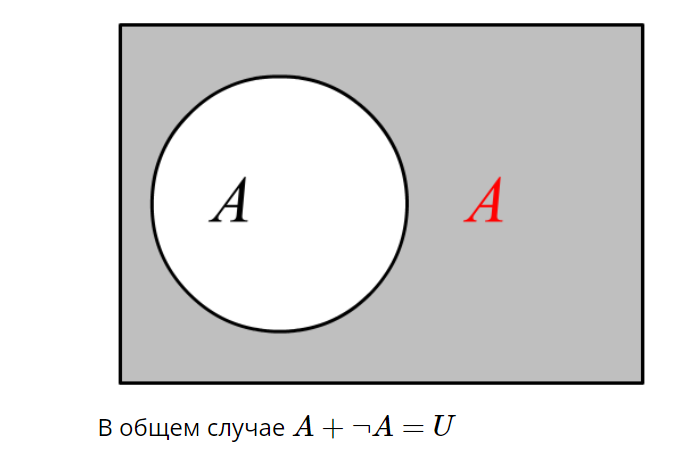
Теперь попробуем разобраться с логической операцией «инверсией», которая является аналогом дополнения в теории множеств.
На диаграмме прямоугольник — это «универсум рассуждения». Переменная
Пусть переменная
Рассмотрим таблицу истинности:
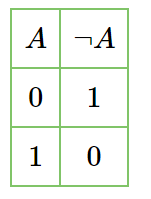
Высказывание
Импликация
В теории множеств соответствующей операции нет. Изобразим импликацию с помощью диаграммы Эйлера — Венна.
Рассмотрим таблицу истинности:
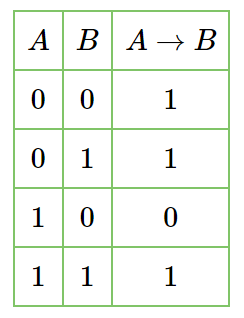
Значение импликации равно «истина» в трёх случаях
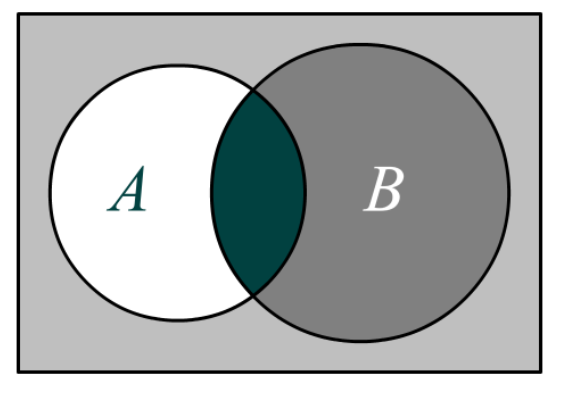
1) область вне двух пересекающихся кругов, которая соответствует значениям
2) область, относящуюся только к кругу
3) область, относящуюся и к кругу
Объединение этих трёх областей и будет графическим представлением логической операции импликации.
Эквивалентность
В теории множеств соответствующей операции нет. Отобразим эквивалентность с помощью диаграммы Эйлера — Венна.
Рассмотрим таблицу истинности:
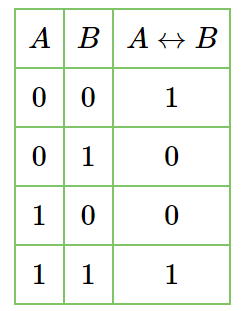
Значение эквивалентности равно «истина» в двух случаях
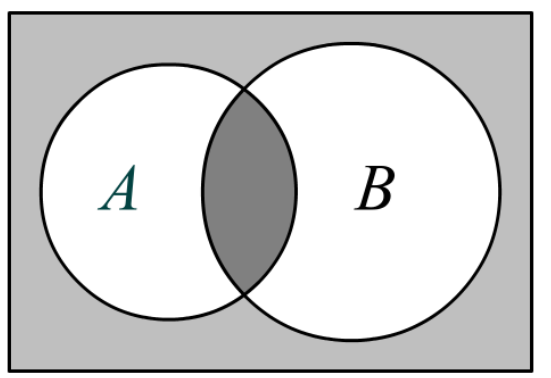
1) область вне двух пересекающихся кругов, которая соответствует значениям
2) область, относящуюся и к кругу
Объединение этих двух областей и будет графическим представлением логической операции эквивалентности.
![[BPKSPO.RU] Moodle](https://distant.bpkspo.ru/moodle/pluginfile.php/1/core_admin/logocompact/300x300/1716258631/%D0%AD%D0%BC%D0%B1%D0%BB%D0%B5%D0%BC%D0%B0%20%D1%81%D0%BE%D0%BA%D1%80%D0%B0%D1%89%D0%B5%D0%BD%D0%BD%D0%B0%D1%8F%20%D0%BF%D1%80%D0%BE%D0%B7%D1%80%D0%B0%D1%87%D0%BD%D0%B0%D1%8F.png)